Chương 05: Tầng mạng: mặt phẳng điều khiển, Bài 02: Các thuật toán định tuyến
Tóm tắt ngắn:
- Video giới thiệu về các thuật toán định tuyến trong mạng máy tính, tập trung vào hai nhóm chính: Link State và Distance Vector.
- Các điểm chính bao gồm mục tiêu của định tuyến (tìm đường đi tốt nhất), mô hình hóa mạng bằng đồ thị, thuật toán Dijkstra (Link State), thuật toán Distance Vector dựa trên phương trình Bellman-Ford, và so sánh hai nhóm thuật toán. Video cũng đề cập đến hiện tượng dao động (oscillation) trong thuật toán Distance Vector và vấn đề lan truyền thông tin sai lệch.
- Ứng dụng chính là việc định tuyến gói tin trong mạng máy tính, đảm bảo gói tin đến đích một cách hiệu quả. Hiệu quả của định tuyến ảnh hưởng trực tiếp đến chất lượng dịch vụ mạng.
- Các quá trình được mô tả chi tiết bao gồm thuật toán Dijkstra (với ví dụ minh họa) và cơ chế hoạt động của thuật toán Distance Vector (với ví dụ minh họa).
Tóm tắt chi tiết:
Video được chia thành các phần chính sau:
Phần 1: Giới thiệu và mục tiêu định tuyến: Video bắt đầu bằng việc giới thiệu khái niệm thuật toán định tuyến (thay vì giao thức định tuyến, vì nội dung tập trung vào thuật toán). Mục tiêu chính là tìm đường đi tốt nhất (đường ngắn nhất, nhanh nhất, ít tắc nghẽn nhất) từ máy gửi đến máy nhận thông qua các router. Người thuyết trình nhấn mạnh tầm quan trọng của định tuyến trong mạng máy tính ("routing là một trong 10 vấn đề đáng quan tâm của mạng máy tính").
Phần 2: Mô hình hóa mạng và chi phí liên kết: Mạng được mô hình hóa bằng đồ thị (graph), với các router là nút (node) và các đường liên kết là cạnh (edge). Chi phí liên kết (link cost) được định nghĩa và có thể dựa trên nhiều yếu tố như băng thông (bandwidth), độ trễ (delay), và mức độ tắc nghẽn (congestion). Người thuyết trình thảo luận về cách định nghĩa chi phí, nhấn mạnh rằng nó phụ thuộc vào người quản trị mạng.
Phần 3: Phân loại thuật toán định tuyến: Thuật toán định tuyến được phân loại theo hai cách: (1) Thông tin toàn cục (global/centralized) hay cục bộ (decentralized): Link State (thông tin toàn cục) và Distance Vector (thông tin cục bộ). (2) Tốc độ thay đổi của mạng: Thuật toán tĩnh (thay đổi chậm) và động (thay đổi nhanh). Video tập trung vào Link State và Distance Vector.
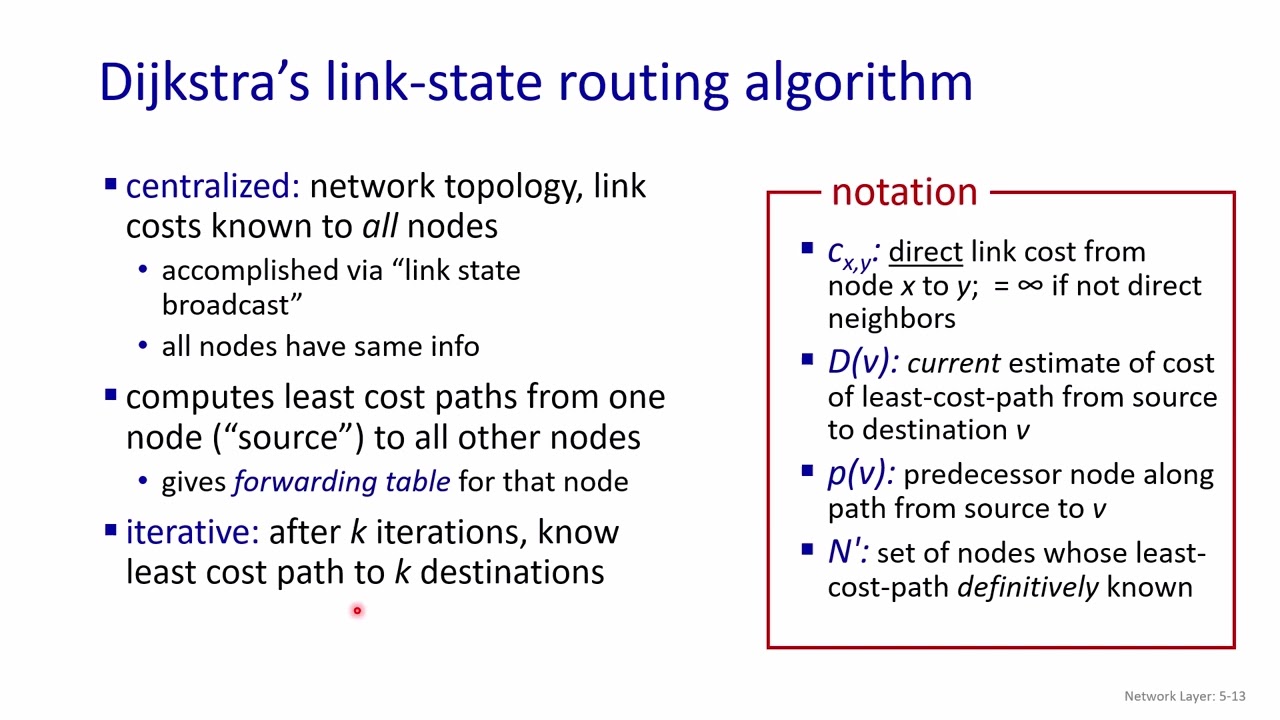
Phần 4: Thuật toán Dijkstra (Link State): Đây là phần chi tiết nhất, giải thích thuật toán Dijkstra với các ký hiệu, pseudocode và hai ví dụ minh họa. Người thuyết trình giải thích từng bước của thuật toán, cách tính toán khoảng cách ngắn nhất và xây dựng bảng chuyển tiếp (forwarding table). Điểm nhấn là việc tìm nút có khoảng cách nhỏ nhất chưa được xét và cập nhật khoảng cách đến các nút lân cận. Video cũng phân tích độ phức tạp của thuật toán (O(n²) và khả năng giảm xuống O(n log n)).
Phần 5: Thuật toán Distance Vector (dựa trên Bellman-Ford): Phần này giới thiệu thuật toán Distance Vector dựa trên phương trình Bellman-Ford, giải thích ý tưởng chính là cập nhật vector khoảng cách dựa trên thông tin từ các hàng xóm. Video nhấn mạnh tính chất phân tán (distributed), không đồng bộ (asynchronous) và khả năng hội tụ của thuật toán. Một ví dụ minh họa được sử dụng để giải thích quá trình cập nhật vector khoảng cách và lan truyền thông tin.
Phần 6: So sánh Link State và Distance Vector, và vấn đề dao động: Video so sánh hai nhóm thuật toán về độ phức tạp, tốc độ hội tụ và độ ổn định. Vấn đề dao động (oscillation) trong thuật toán Distance Vector được minh họa bằng một ví dụ, cho thấy khả năng thuật toán không hội tụ và thay đổi đường đi liên tục. Vấn đề lan truyền thông tin sai lệch trong Distance Vector cũng được đề cập.
Phần 7: Kết luận: Video kết thúc bằng tóm tắt các điểm chính, nhấn mạnh sự khác biệt giữa hai nhóm thuật toán và đề cập đến các vấn đề cần xem xét khi áp dụng chúng trong thực tế.