Thống kê_Buổi 3_ver record của meet - 720p

Tóm tắt ngắn:

Bài giảng tập trung vào khái niệm xác suất, đặc biệt là xác suất có điều kiện và các định lý liên quan.
Các điểm chính bao gồm định nghĩa xác suất có điều kiện, công thức tính, quy tắc nhân, khái niệm biến cố độc lập, định lý Bayes, và ứng dụng vào các bài toán thực tế như đầu tư, phân biệt đối xử giới tính trong thăng chức, và dự đoán kết quả dự án. Các ví dụ cụ thể được sử dụng để minh họa, bao gồm ví dụ về đầu tư, phân tích dữ liệu về thăng chức, và dự án trung tâm mua sắm.
Xác suất được ứng dụng rộng rãi trong nhiều lĩnh vực, từ tài chính, nhân sự đến quy hoạch và dự đoán. Việc hiểu rõ xác suất có điều kiện và định lý Bayes giúp cập nhật thông tin và đưa ra quyết định chính xác hơn.
Phương pháp được trình bày chi tiết bao gồm cách tính xác suất có điều kiện, quy tắc nhân, cách xác định biến cố độc lập, và ứng dụng định lý Bayes để cập nhật xác suất.

Tóm tắt chi tiết:

Bài giảng được chia thành các phần chính sau:

Phần 1: Xác suất có điều kiện và quy tắc nhân: Phần này giới thiệu định nghĩa xác suất có điều kiện P(A|B) = P(A giao B) / P(B), và quy tắc nhân: P(A giao B) = P(A)P(B|A) = P(B)P(A|B). Giảng viên nhấn mạnh việc ghi nhớ công thức và khả năng tưởng tượng để hiểu rõ hơn. Các ví dụ về đầu tư (đầu tư vào mắt bay có lãi, đầu tư vào cổ phiếu có lãi) được sử dụng để minh họa.

Phần 2: Biến cố độc lập: Phần này định nghĩa biến cố độc lập: P(A|B) = P(A) và P(B|A) = P(B). Giảng viên giải thích cách sử dụng quy tắc nhân để kiểm tra tính độc lập của hai biến cố. Ví dụ về đầu tư được sử dụng lại để minh họa việc kiểm tra tính độc lập của hai biến cố.

Phần 3: Định lý Bayes: Phần này giới thiệu định lý Bayes như một công cụ để cập nhật xác suất dựa trên thông tin mới. Công thức và quy trình cập nhật xác suất được giải thích. Ví dụ về dự án trung tâm mua sắm (chấp thuận của chính quyền địa phương và ủy ban kế hoạch) được sử dụng để minh họa cách áp dụng định lý Bayes. Giảng viên nhấn mạnh tầm quan trọng của việc hiểu quy trình cập nhật xác suất.

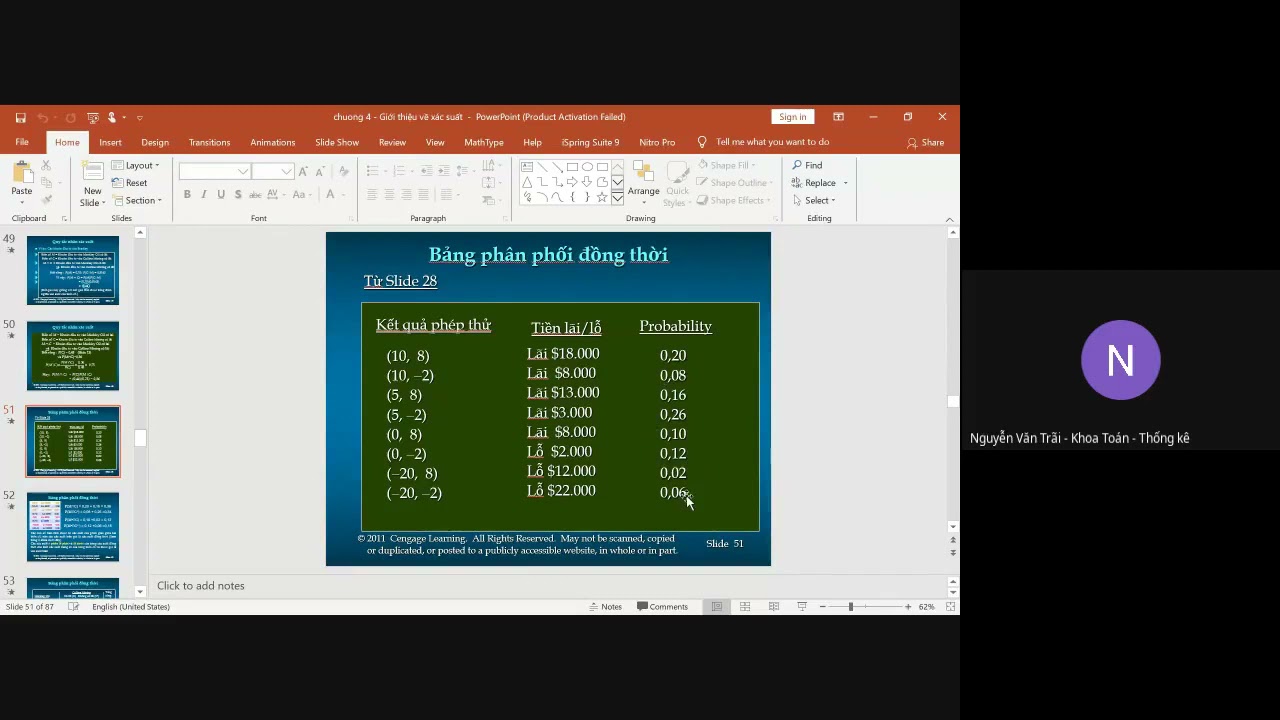
Phần 4: Phân phối xác suất: Phần này giới thiệu khái niệm biến ngẫu nhiên rời rạc và liên tục, cùng với cách mô tả phân phối xác suất của chúng (bằng bảng, công thức, đồ thị). Phân phối nhị thức được giải thích chi tiết, kèm theo công thức và ví dụ về xác suất khách hàng mua hàng. Giảng viên nhấn mạnh việc hiểu rõ các khái niệm và công thức.

Phần 5: Giá trị kỳ vọng và phương sai: Phần này định nghĩa giá trị kỳ vọng (E(X)) và phương sai (Var(X)) của biến ngẫu nhiên rời rạc, kèm theo công thức tính toán. Ví dụ về bán ô tô được sử dụng để minh họa.

Phần 6: Phân phối chuẩn: Phần này giới thiệu phân phối chuẩn, đặc điểm của nó (đối xứng, trung bình = trung vị = mốt, độ lệch chuẩn xác định độ rộng), và cách sử dụng bảng phân phối chuẩn để tính xác suất. Ví dụ về lượng dầu dự trữ được sử dụng để minh họa cách tính xác suất sử dụng phân phối chuẩn. Giảng viên nhấn mạnh tầm quan trọng của phân phối chuẩn trong thống kê.

Phần 7: Xấp xỉ chuẩn của phân phối nhị thức: Phần này giải thích cách sử dụng phân phối chuẩn để xấp xỉ phân phối nhị thức khi số phép thử lớn. Điều kiện áp dụng (np ≥ 5 và n(1-p) ≥ 5) và công thức điều chỉnh tính liên tục được nhấn mạnh. Ví dụ về xác suất lỗi trong hóa đơn được sử dụng để minh họa.

Phần 8: Phân phối mũ: Phần này giới thiệu phân phối mũ, đặc điểm và cách tính xác suất. Ví dụ về thời gian giữa các lần xe đến trạm thu phí được sử dụng để minh họa.

Phần 9: Câu hỏi và thảo luận: Phần cuối cùng dành cho câu hỏi và thảo luận của sinh viên, bao gồm các câu hỏi về bài toán 3 cánh cửa của Monty Hall, bài tập về nhà, và hướng dẫn về báo cáo dự án.

Giảng viên thường xuyên nhắc nhở sinh viên ghi nhớ công thức, hiểu rõ quy trình, và vận dụng kiến thức vào các bài toán thực tế. Nhiều ví dụ cụ thể được sử dụng để minh họa các khái niệm và phương pháp. Bài giảng kết thúc bằng phần hỏi đáp và hướng dẫn về báo cáo dự án cuối kỳ.