Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 14.2 - Erdos Renyi Random Graphs
Short Summary:
This lecture introduces the Erdős-Rényi (ER) random graph model (GNP and GNM variants) as a baseline for understanding real-world networks. Key properties of ER graphs, like degree distribution (binomial), clustering coefficient (low), average path length (logarithmic), and connectivity (giant component emerges when average degree > 1), are mathematically analyzed and compared to the properties of the MSN network (Microsoft social network). The comparison reveals significant discrepancies, demonstrating that real-world networks are not well-represented by the simple ER model. The lecture highlights the limitations of the ER model, particularly its inability to capture the skewed degree distribution, high clustering coefficient, and local structure observed in real networks. Despite its limitations, the ER model serves as a valuable null model for comparison and analysis.
Detailed Summary:
The lecture is divided into several sections:
1. Introduction to Erdős-Rényi Random Graphs: The lecture begins by introducing the Erdős-Rényi (ER) random graph model as a generative model for graphs, serving as a reference point for comparison with real-world networks. Two variants are presented: G(n,p) (each edge appears independently with probability p) and G(n,m) (a graph with n nodes and m edges chosen uniformly at random). Both models are stochastic, meaning multiple graphs can be generated for the same parameters (n and p or m). An example with n=10 and p=1/6 is shown, illustrating the stochastic nature of the model.
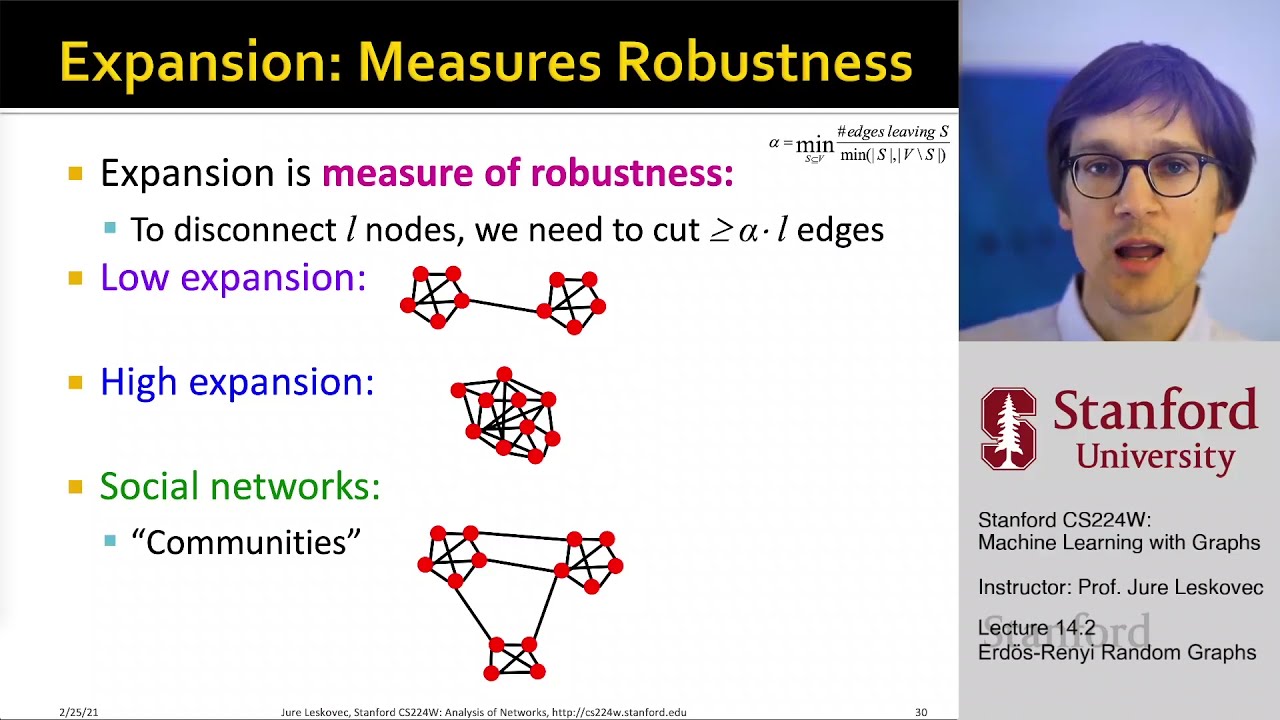
2. Mathematical Analysis of G(n,p) Properties: The lecture focuses on analyzing the properties of the G(n,p) model. The degree distribution is shown to be binomial, with an average degree of approximately np. The clustering coefficient is derived and shown to be approximately the average degree divided by the number of nodes (n), implying a very low clustering coefficient for large graphs. The connectivity of the graph is discussed, showing a phase transition: a giant connected component emerges when the average degree exceeds one. A simulation demonstrates this phase transition. The average path length is also discussed, relating it to the concept of graph expansion. High expansion leads to short average path lengths, which are shown to be logarithmic in the number of nodes for ER graphs with sufficiently high average degree.
3. Comparison with the MSN Network: The properties of the ER model (degree distribution, clustering coefficient, average path length, and connectivity) are compared to those of the MSN network. Significant discrepancies are highlighted: the MSN network exhibits a heavily skewed degree distribution, a much higher clustering coefficient than predicted by the ER model, and a similar average path length. This comparison demonstrates that the MSN network is not well-represented by the ER model. The statement "clearly, MSN and GMP can match MSN in terms of shortest path lengths, in terms of connectivity; it totally misses clustering, it totally misses degree distribution" summarizes the key differences.
4. Limitations of the ER Model and Future Directions: The lecture concludes by discussing the limitations of the ER model. Its inability to capture the skewed degree distribution, high clustering coefficient, and local structure (lack of "friend of a friend" effect) of real-world networks is emphasized. Despite these limitations, the ER model remains a valuable null model for comparison. The lecture suggests that more sophisticated models are needed to accurately represent real-world networks. The speaker notes that the properties observed in the MSN network are common across a wide range of real-world networks.