Link to original video by Movies Interesting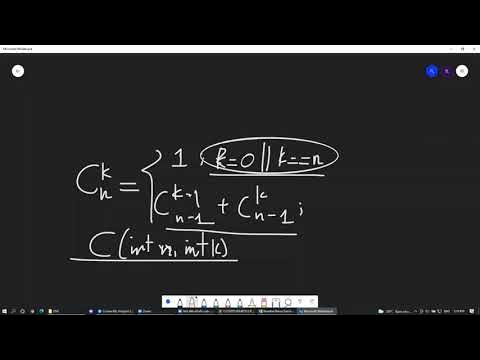

Buổi 1: Lý thuyết số

Tóm tắt video "Buổi 1: Lý thuyết số"

Tóm tắt ngắn:

• Video giới thiệu về các khái niệm cơ bản trong lý thuyết số, bao gồm sàng số nguyên tố, phân tích thừa số nguyên tố, ước chung lớn nhất, bội chung nhỏ nhất, đồng dư, lũy thừa nhị phân, cấp số cộng, cấp số nhân, tổ hợp, chỉnh hợp, và công thức Legendre.
• Video thảo luận về các kỹ thuật và công thức liên quan đến các khái niệm này, ví dụ như sàng số nguyên tố, công thức tính số ước, tính tích các ước, công thức tính ước chung lớn nhất, bội chung nhỏ nhất, các công thức đồng dư, lũy thừa nhị phân, công thức tính tổng cấp số cộng, cấp số nhân, công thức tổ hợp, chỉnh hợp, và công thức Legendre.
• Video nhấn mạnh tầm quan trọng của các khái niệm này trong việc giải quyết các bài toán liên quan đến lý thuyết số, đặc biệt là các bài toán có kết quả lớn hoặc yêu cầu tính toán số dư.
• Video trình bày chi tiết các phương pháp và thuật toán để thực hiện các phép tính liên quan đến các khái niệm được thảo luận, bao gồm sàng số nguyên tố, phân tích thừa số nguyên tố, tính ước chung lớn nhất, bội chung nhỏ nhất, lũy thừa nhị phân, và công thức Legendre.

Tóm tắt chi tiết:

Phần 1: Sàng số nguyên tố

• Giới thiệu về sàng số nguyên tố và ứng dụng của nó trong việc liệt kê, đếm, hoặc kiểm tra số nguyên tố trong một khoảng cho trước.
• Trình bày thuật toán sàng số nguyên tố sử dụng mảng đánh dấu, với độ phức tạp O(n log log n).
• Nhấn mạnh hạn chế của thuật toán sàng số nguyên tố khi n lớn (khoảng 10^7).
• Cung cấp ví dụ minh họa cách sử dụng sàng số nguyên tố để tìm các số nguyên tố trong khoảng từ 1 đến 10^7.

Phần 2: Phân tích thừa số nguyên tố

• Nhắc lại cách phân tích thừa số nguyên tố của một số tự nhiên.
• Giới thiệu hai công thức quan trọng có thể suy ra từ phân tích thừa số nguyên tố:
  • Công thức tính số lượng ước của một số (hàm DN).
  • Công thức tính tích các ước của một số (hàm Phi n).
• Minh họa cách sử dụng hai công thức này với ví dụ cụ thể.

Phần 3: Ước chung lớn nhất và bội chung nhỏ nhất

• Nhắc lại thuật toán Euclid để tính ước chung lớn nhất của hai số.
• Giới thiệu công thức tính bội chung nhỏ nhất của hai số dựa trên ước chung lớn nhất.
• Nhấn mạnh hạn chế của công thức tính bội chung nhỏ nhất khi hai số quá lớn và cách khắc phục bằng cách chia trước khi nhân.
• Cung cấp ví dụ minh họa cách tính ước chung lớn nhất và bội chung nhỏ nhất của nhiều số.

Phần 4: Đồng dư

• Giới thiệu khái niệm đồng dư và bốn công thức cơ bản về đồng dư:
  • Cộng, trừ, nhân, và lũy thừa.
• Giải thích chi tiết từng công thức và minh họa bằng ví dụ cụ thể.
• Nhấn mạnh tầm quan trọng của việc sử dụng các công thức đồng dư để giải quyết các bài toán có kết quả lớn hoặc yêu cầu tính toán số dư.
• Cung cấp ví dụ minh họa cách sử dụng các công thức đồng dư để tính tổng, tích, hoặc lũy thừa của nhiều số và chia dư cho một số cho trước.

Phần 5: Lũy thừa nhị phân

• Giới thiệu thuật toán lũy thừa nhị phân để tính a^b với độ phức tạp O(log b).
• Trình bày hai cách code thuật toán lũy thừa nhị phân:
  • Sử dụng đệ quy.
  • Sử dụng vòng lặp và biểu diễn nhị phân của b.
• Giải thích tại sao thuật toán lũy thừa nhị phân hiệu quả hơn so với cách duyệt từ 1 đến b.
• Minh họa cách sử dụng thuật toán lũy thừa nhị phân để tính a^b và chia dư cho một số cho trước.

Phần 6: Cấp số cộng và cấp số nhân

• Nhắc lại khái niệm cấp số cộng và cấp số nhân.
• Trình bày công thức tính số hạng thứ n và tổng n số hạng đầu tiên của cấp số cộng và cấp số nhân.
• Minh họa cách sử dụng các công thức này với ví dụ cụ thể.

Phần 7: Tổ hợp, chỉnh hợp, và multinomial coefficient

• Giới thiệu khái niệm tổ hợp, chỉnh hợp, và multinomial coefficient.
• Trình bày công thức tính tổ hợp, chỉnh hợp, và multinomial coefficient.
• Minh họa cách sử dụng các công thức này với ví dụ cụ thể.

Phần 8: Công thức Legendre

• Giới thiệu công thức Legendre để tính bậc của một số nguyên tố trong n!.
• Trình bày hai cách tính bậc của một số nguyên tố trong n!:
  • Sử dụng vòng lặp.
  • Sử dụng công thức Legendre.
• Nhấn mạnh ưu điểm của công thức Legendre về tốc độ tính toán.
• Cung cấp ví dụ minh họa cách sử dụng công thức Legendre để tính bậc của một số nguyên tố trong n!.

Kết luận:

• Video kết thúc bằng việc nhắc lại các kiến thức đã được thảo luận và giới thiệu các kiến thức sẽ được học trong buổi sau, bao gồm giải thuật Euclid mở rộng, nghịch đảo modulo, định lý Euler, hàm Euler, bài toán chia kẹo của Euler, và nguyên lý bù trừ.
• Video khuyến khích người xem về nhà làm bài tập và đặt câu hỏi nếu có bất kỳ thắc mắc nào.
• Video thông báo về lịch học tiếp theo và các chủ đề sẽ được thảo luận trong các buổi học tiếp theo.