Link to original video by The Math Sorcerer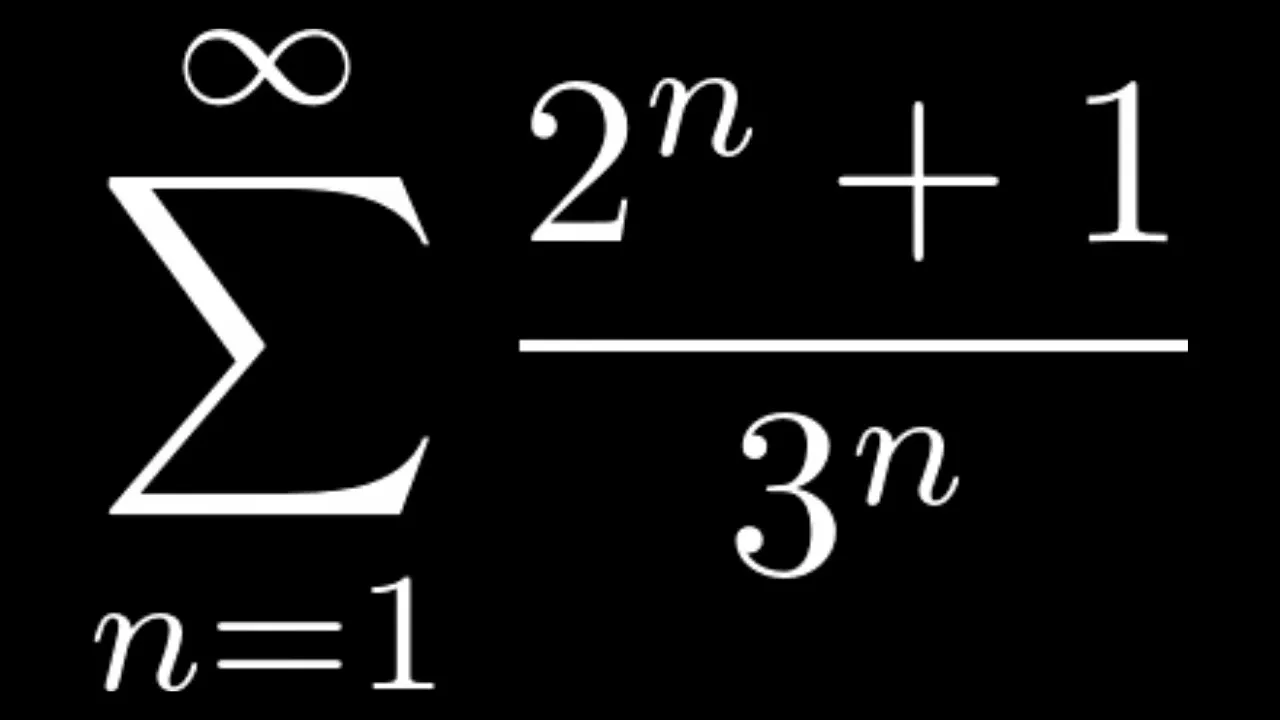
Find the Sum of the Series SUM((2^n + 1)/3^n)
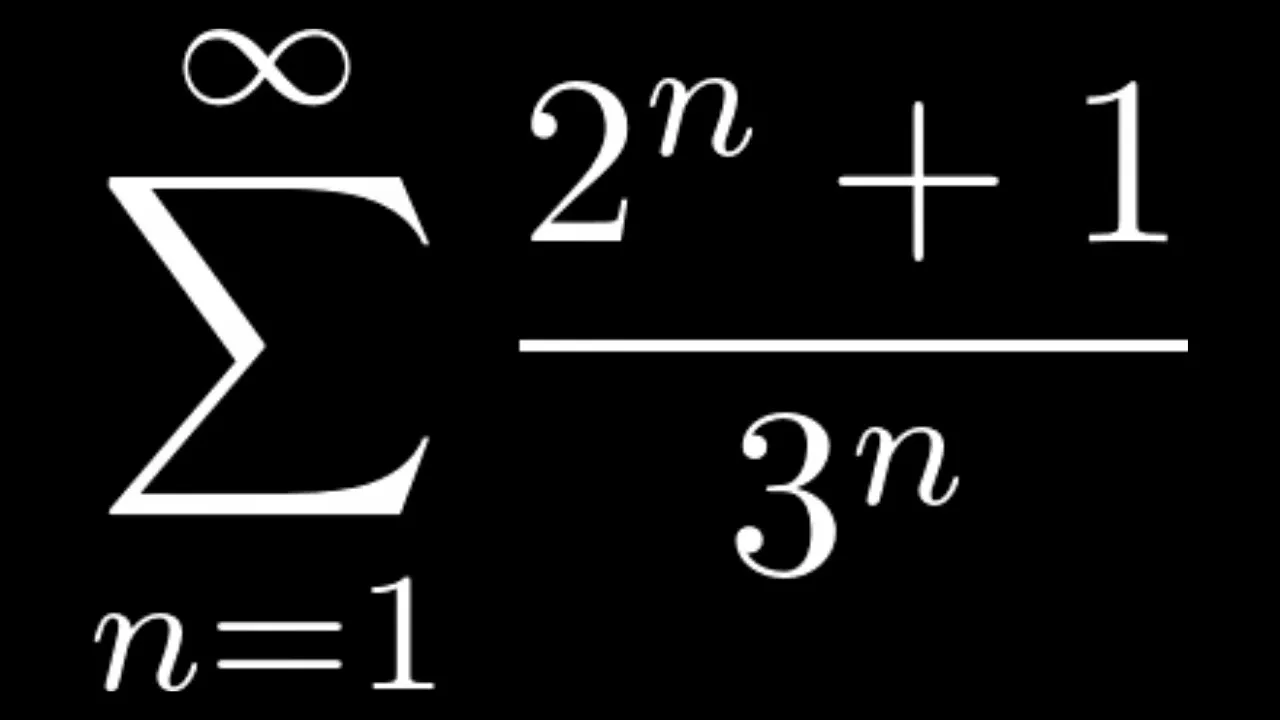
Tóm tắt video:
Tóm tắt ngắn:
- Video hướng dẫn cách tìm tổng của chuỗi vô hạn SUM((2^n + 1)/3^n) bằng cách tách chuỗi thành hai chuỗi hình học vô hạn.
- Video giải thích về khái niệm chuỗi hình học vô hạn, điều kiện hội tụ và công thức tính tổng.
- Video áp dụng công thức để tính tổng của hai chuỗi hình học vô hạn và kết quả cuối cùng là 5/2.
Tóm tắt chi tiết:
Phần 1: Giới thiệu bài toán
- Video giới thiệu bài toán tìm tổng của chuỗi vô hạn SUM((2^n + 1)/3^n).
- Người dẫn chương trình giải thích cách tiếp cận bài toán bằng cách tách chuỗi thành hai chuỗi hình học vô hạn.
Phần 2: Tách chuỗi thành hai chuỗi hình học vô hạn
- Video giải thích cách tách (2^n + 1)/3^n thành 2^n/3^n + 1/3^n.
- Sử dụng tính chất của lũy thừa để viết lại 2^n/3^n thành (2/3)^n và 1/3^n thành (1/3)^n.
- Video khẳng định rằng hai chuỗi mới tạo thành là chuỗi hình học vô hạn.
Phần 3: Giới thiệu về chuỗi hình học vô hạn
- Video giới thiệu khái niệm chuỗi hình học vô hạn và công thức tính tổng.
- Người dẫn chương trình giải thích rằng chuỗi hình học vô hạn hội tụ khi giá trị tuyệt đối của công bội (r) nhỏ hơn 1.
- Video xác định công bội của hai chuỗi hình học vô hạn là 2/3 và 1/3, cả hai đều nhỏ hơn 1, do đó hai chuỗi hội tụ.
Phần 4: Áp dụng công thức tính tổng
- Video áp dụng công thức tính tổng chuỗi hình học vô hạn cho hai chuỗi đã tách.
- Công thức được sử dụng là: tổng = a/(1-r), trong đó a là số hạng đầu tiên và r là công bội.
- Video tính tổng của hai chuỗi và kết quả cuối cùng là 5/2.
Phần 5: Kết luận
- Video kết thúc bằng cách khẳng định rằng 5/2 là tổng của chuỗi vô hạn SUM((2^n + 1)/3^n).
- Người dẫn chương trình hy vọng video hữu ích cho người xem.