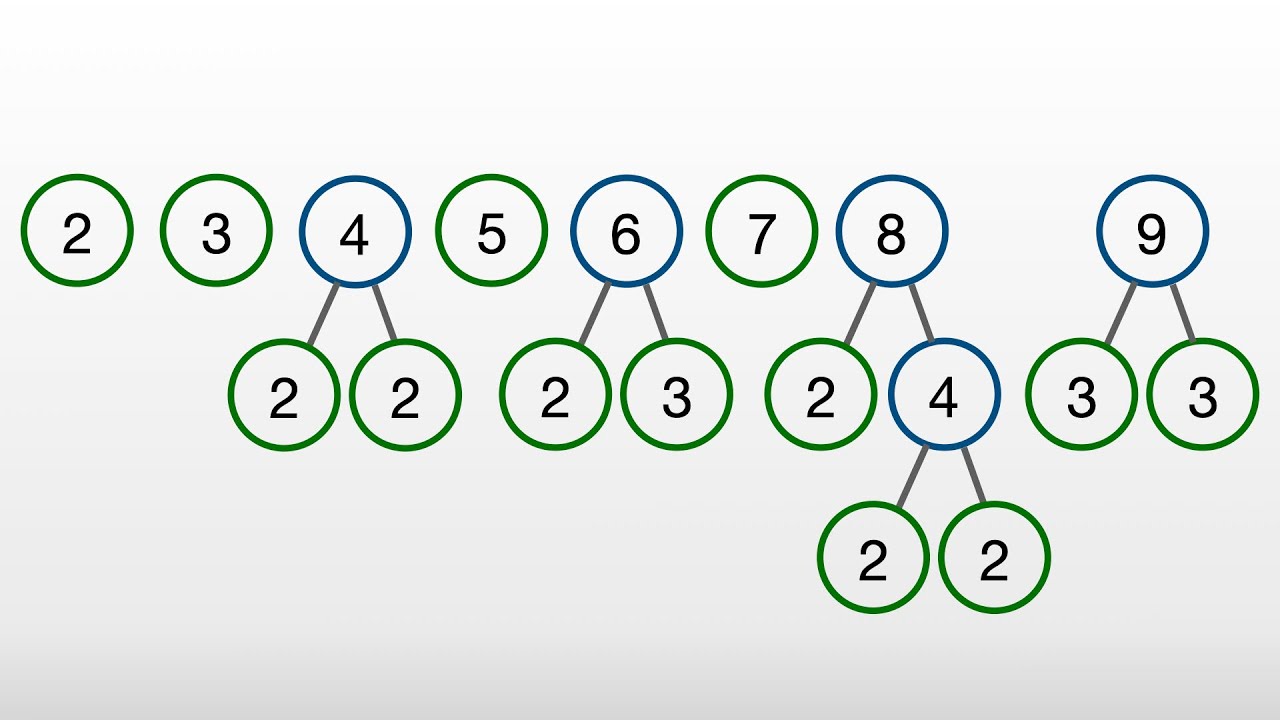
The Fundamental Theorem of Arithmetic

Zusammenfassung des Videos "Der Fundamentalsatz der Arithmetik"

Kurze Zusammenfassung:

Das Video erklärt den Fundamentalsatz der Arithmetik, der besagt, dass jede natürliche Zahl größer als 1 entweder eine Primzahl ist oder sich als Produkt von Primzahlen darstellen lässt.
Es werden Beispiele für Primzahlen und zusammengesetzte Zahlen gegeben und die eindeutige Faktorisierung von Zahlen in Primzahlen erläutert.
Der Beweis für die Eindeutigkeit der Primfaktorisierung wird anhand eines Widerspruchsbeweises dargestellt.
Der Vergleich von Primzahlen mit Atomen in der Chemie verdeutlicht die fundamentale Bedeutung von Primzahlen in der Zahlentheorie.

Detaillierte Zusammenfassung:

1. Einführung:

Das Video beginnt mit der Analogie zwischen Atomen und Primzahlen.
Es wird erklärt, dass jede Zahl entweder eine Primzahl ist oder sich als Produkt von Primzahlen darstellen lässt.
Primzahlen sind Zahlen, die nur durch 1 und sich selbst teilbar sind (z.B. 2, 3, 5, 7).
Zusammengesetzte Zahlen sind Zahlen, die sich als Produkt von zwei oder mehr Zahlen darstellen lassen (z.B. 12 = 2 x 2 x 3).

2. Der Fundamentalsatz der Arithmetik:

Der Fundamentalsatz der Arithmetik besagt, dass jede natürliche Zahl größer als 1 entweder eine Primzahl ist oder sich als Produkt von Primzahlen darstellen lässt.
Diese Faktorisierung ist eindeutig, d.h. es gibt nur eine einzige Möglichkeit, eine Zahl in Primzahlen zu zerlegen.

3. Beispiel: Primfaktorisierung von 90:

Das Video demonstriert die Primfaktorisierung der Zahl 90.
Es wird gezeigt, wie man Schritt für Schritt die kleinsten Primzahlen findet, die 90 teilen, bis man die Primfaktoren 2, 3, 3 und 5 erhält.

4. Beweis der Eindeutigkeit:

Der Beweis für die Eindeutigkeit der Primfaktorisierung erfolgt durch einen Widerspruchsbeweis.
Es wird angenommen, dass es zwei verschiedene Primfaktorisierungen einer Zahl x gibt.
Durch Division beider Seiten der Gleichung durch die Primzahlen der ersten Faktorisierung wird gezeigt, dass die Primzahlen der zweiten Faktorisierung mit den Primzahlen der ersten Faktorisierung übereinstimmen müssen.
Dies widerspricht der Annahme, dass die beiden Faktorisierungen unterschiedlich sind.

5. Schlussfolgerung:

Das Video fasst zusammen, dass Primzahlen die "Atome" der Zahlen sind.
Ohne Primzahlen gäbe es keine anderen Zahlen.
Der Fundamentalsatz der Arithmetik ist ein grundlegendes Prinzip der Zahlentheorie und hat weitreichende Anwendungen in verschiedenen Bereichen der Mathematik und Informatik.